通学路の組み合わせ総数
みなさんは通学路をいくつ持っていますか?
パッと答えられなかったアナタは、自分の通学路の個数、知りたくありませんか?
私はとても知りたい! というのも、私は現在兵庫県の某所から京都市の大学に2時間前後かけて通学しているため、通学路が複数存在しているのです。
普段は定期を使って決まったルートを通学するのみですが、定期が切れたときはここぞとばかりに様々なルートで通っています。そんなルートの総数、知りたいですよね?
前提条件
ルートの総数を求める上でいくつか前提条件を設けます。
そうしないとルートの数が無限大に発散したり、天文学的な数字になってしまうからです。
前提1. グラフで考える
ルートをグラフで考えることにします。
グラフとはグラフ理論のグラフです。
例えば自宅から駅への徒歩を考えたとき、曲がる交差点を変えたりすれば無数にルートを生み出せますが、面白くないので自宅→駅の徒歩移動は1通りとしたいと思います。グラフを利用するとこうした単純化を行うことができます。
以下のようなグラフを考えます。
- 頂点
- 自宅
- 駅
- 終点
- 乗換駅
- 自宅・大学の最寄駅
- バス停
- バス停以外の頂点の最寄り(同一頂点に最寄りが複数存在する場合もある)
- 大学
- 枝
- 徒歩
- 鉄道路線(含:新幹線)
- バス路線
このグラフは有向グラフで、特にDAGとなるように構築します。
問題の特性上、入次数が0の頂点(始点)は自宅のみ、出次数が0の頂点(終点)は大学のみとなります。
ルートをグラフとして表現することで、問題をシンプルに表すことができました。
前提2. グラフの枝は独断で
頂点同士を枝で結ぶかどうかの基準は独断で決めたいと思います。
極端な話、徒歩で大学まで通ったり(70km超)できてしまうので、最短の通学時間である2時間弱からあまりに離れたルートを選べないように枝を張ります。
問題設定
以上の前提を踏まえると次のような問題を解けばいいことがわかります。
DAGにおける始点から終点への経路の数え上げ
あとはグラフさえ定義できてしまえば解けますね!
グラフの定義
グラフを描画してみました。
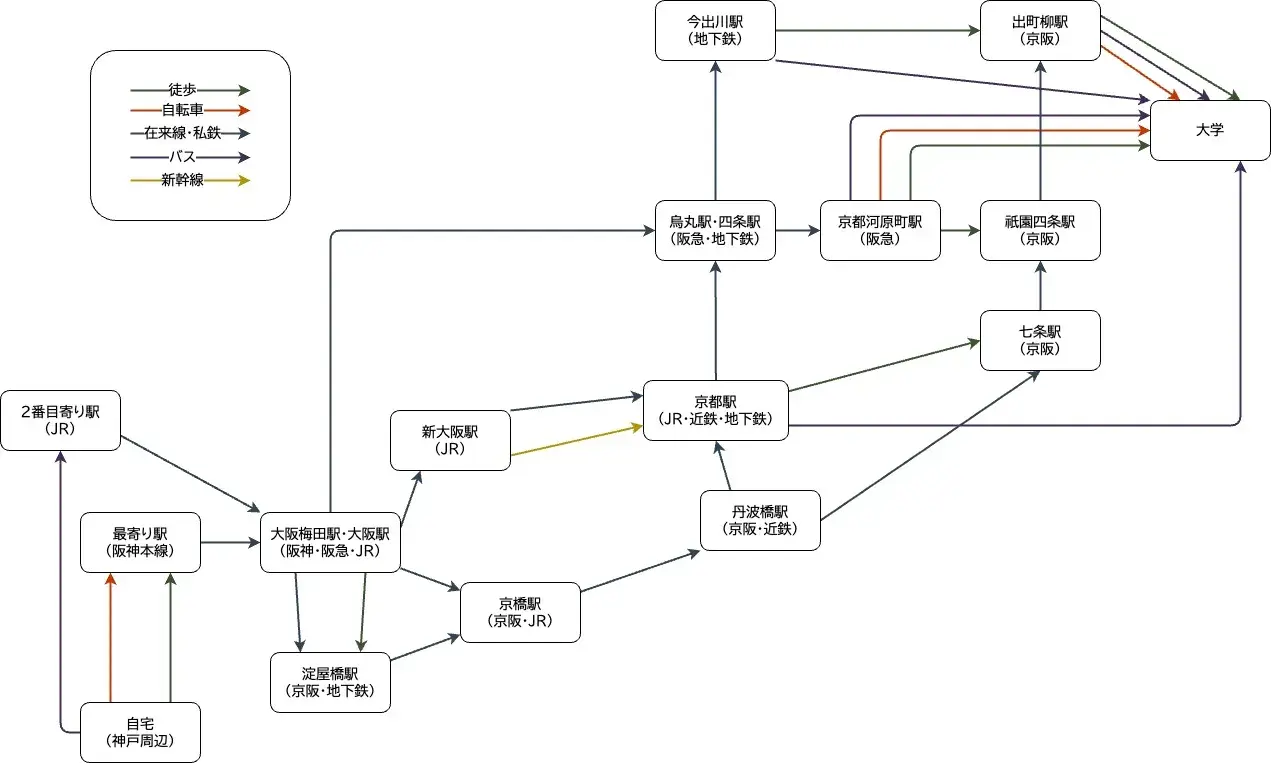
先程述べたように、グラフの枝や頂点は独断で決定しました。
自宅から最寄り駅まではバス移動も可能ですが、まずしないので除外したり、烏丸や七条からも大学に直行するバスがあるはずですが、ほぼ使わないので除外したりしています。
あとは「最寄り→尼崎→鶴橋→京橋」をはじめとして大阪市内のルートはたくさん考えられますが、ややこしいので除外しています。
そのくせして新大阪から京都までの新幹線は含めたりしています。
自宅から矢印の方向にたどっていくと、どのルートを通っても大学にたどり着くようになっているはずです。これはDAGになるよう構築したためです。
経路の総数を求める
経路の総数の求め方は次のとおりです。
- 自宅までの経路の総数を1とする
- 自身を指す矢印を持つ頂点までの経路の総数が確定したような頂点の経路の総数を、自身を指す矢印を持つ頂点の経路の総数の総和とする
- を大学に到着するまで繰り返す
2. がややこしいですが手計算した結果の画像をお見せするのでなんとなくわかっていただけると思います。
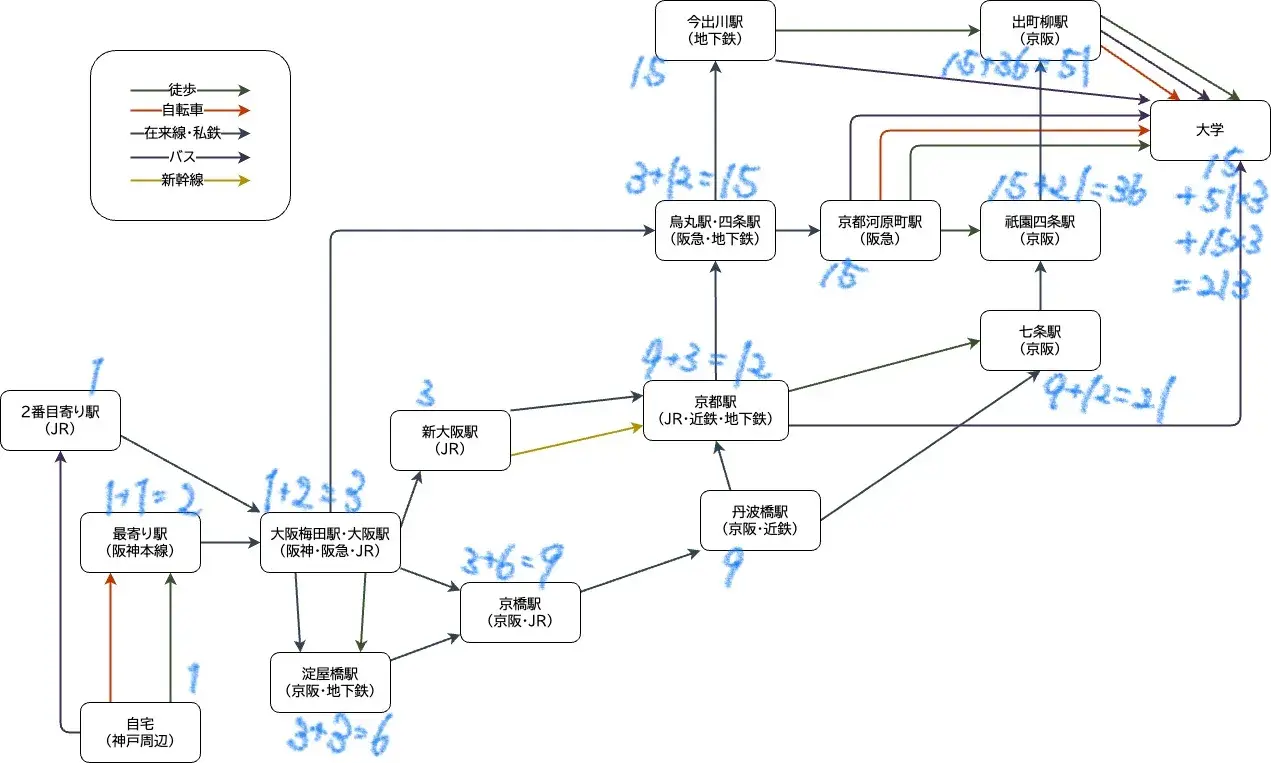
結果はなんと213通りとなりました!!!
大学の授業は前後期それぞれ15週(含テスト)なので毎日大学に通ったとしても、前後期合わせて回しか大学に行く機会がなく、1年かけてもすべての組み合わせを試すことができません。授業以外の課外活動などで通学する場合はその限りではありませんが。
私はこのルートの中でもまだ20個ぐらいしか実践できていないまま4回生の前期を終えてしまいました。
自分の通学路の可能性の幅を数字という形で見せられると、後期の通学が楽しみになってきました。
新幹線通学は一度やってみたいと思っています!
長距離通学で疲弊しているみなさん、長距離ならではの楽しみを見出してみてはいかがでしょうか? 毎日の通学が少し楽しくなるかも。